1330. Nearest
Common Ancestors
A rooted tree is a well-known data
structure in computer science and engineering. An example is shown below:
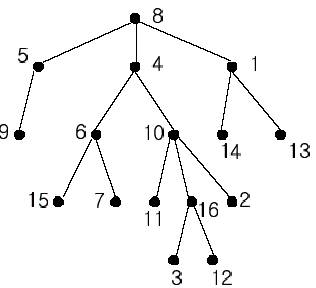
In the figure, each node is labeled
with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is
an ancestor of node y if node x is in the path between the root and node y. For
example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node
16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16.
Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the
ancestors of node 7. A node x is called a common ancestor of two different
nodes y and z if node x is an ancestor of node y and an ancestor of node z.
Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is
called the nearest common ancestor of nodes y and z if x is a common ancestor
of y and z and nearest to y and z among their common ancestors. Hence, the
nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes
16 and 7 than node 8 is.
For other examples, the nearest
common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of
nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is
node 4. In the last example, if y is an ancestor of z, then the nearest common
ancestor of y and z is y.
Write a program that finds the
nearest common ancestor of two distinct nodes in a tree.
Input. The input
consists of T test cases. The number of test cases (T) is given in the first line
of the input file. Each test case starts with a line containing an integer N ,
the number of nodes in a tree, 2 ≤ N ≤ 10,000. The nodes are labeled with integers 1, 2,...,
N. Each of the next N – 1 lines contains a pair of integers that represent an edge
--the first integer is the parent node of the second integer. Note that a tree
with N nodes has exactly N – 1 edges. The
last line of each test case contains two distinct integers whose nearest common
ancestor is to be computed.
Output. Print
exactly one line for each test case. The line should contain the integer that
is the nearest common ancestor.
|
Ïðèìåð âõîäà |
Ïðèìåð âûõîäà |
|
2 16 1 14 8 5 10 16 5 9 4 6 8 4 4 10 1 13 6 15 10 11 6 7 10 2 16 3 8 1 16 12 16 7 5 2 3 3 4 3 1 1 5 3 5 |
4 3 |
ÐÅØÅÍÈÅ
LCA
Àíàëèç àëãîðèòìà
Äëÿ
çàäàííîãî äåðåâà ñëåäóåò íàéòè LCA äâóõ
âåðøèí.
Ðåàëèçàöèÿ àëãîðèòìà
#include <cstdio>
#include <vector>
#include <cstring>
#define MAX
10010
#define
LOGMAX 14
using namespace std;
int i, n,
tests, root, l, x, y, lca;
vector<int> g[MAX];
int
timer, d[MAX], used[MAX], f[MAX];
int
up[MAX][LOGMAX];
void dfs (int v, int p)
{
int i, to;
d[v] = timer++;
up[v][0] = p;
for(i = 1; i
<= l; i++)
up[v][i] = up[up[v][i-1]][i-1];
for(i = 0; i
< g[v].size(); i++)
{
to = g[v][i];
if (to !=
p) dfs (to, v);
}
f[v] = timer++;
}
// if a is a parent of b
int
Parent(int a, int
b)
{
return (d[a]
<= d[b]) && (f[a] >= f[b]);
}
int LCA (int a, int b)
{
if (Parent(a,
b)) return a;
if (Parent(b,
a)) return b;
for (int i = l; i >= 0; i--)
if
(!Parent(up[a][i], b)) a = up[a][i];
return
up[a][0];
}
int main(void)
{
scanf("%d",&tests);
while(tests--)
{
scanf("%d",&n);
l = 1;
while ((1
<< l) <= n) l++;
memset(used,0,sizeof(used));
for(i = 1;
i <= n; i++)
g[i].clear();
memset(d,0,sizeof(d));
memset(f,0,sizeof(f));
memset(up,0,sizeof(up));
for(i = 1;
i < n; i++)
{
scanf("%d
%d",&x,&y);
g[x].push_back(y);
used[y] = 1;
}
for(i = 1;
i <= n; i++)
if
(!used[i]) root = i;
dfs(root,root);
scanf("%d
%d",&x,&y);
lca = LCA(x, y);
printf("%d\n",lca);
}
return 0;
}